
경제학을 공부하려면 직선의 기울기에 대한 이해는 필수입니다.
하지만 중학교 수학을 공부하지 않은 수포자분들은 이 개념을 모를 수도 있어요.
그런 분들을 위해, 아래의 순서로 직선의 기울기에 대해 알려드릴게요.
목차
1. 테스트
2. 오늘 배울 개념
3. 개념 설명
4. 정리
5. 응용문제
혹시 그래프 그리는 방법을 모르는 분들은 아래 포스팅을 먼저 보고 와주세요.
순서쌍 뜻, 그래프 그리는 방법(기초)
그래프를 모른다면, 경제학을 공부할 수 없습니다. 정말 자주 등장하는 개념이기 때문이죠. 경제학 책을 한 번만 훑어봐도 수많은 그래프를 보실 수 있을 거예요. 오늘은 아래의 순서로 그래프
helpmathquitter.tistory.com
그래프를 그릴 줄 안다는 전제하에 알려드릴 테니까요.
1. 테스트
문제를 통해 기울기에 대해 알고 있는지 테스트해 볼까요?
🙆 답을 정확히 아는 분들은 시간 아까우니 당장 이 페이지를 나가서 다른 공부를 하시고,
🙅 답을 모르는 분들, 헷갈리는 분들만 이 글을 정독해 주세요.
✍️ 문제
①~④ 중 (2, 3), (7, 6)을 지나는 직선의 기울기는?

답을 확실하게 말할 수 없는 분들만 이 글을 읽어주세요.
2. 오늘 배울 개념
저와 함께 직선의 기울기에 관해 공부하면, 위 문제를 정확하게 풀 수 있어요.
오늘 배울 개념은 다음과 같습니다.
💡 기울기, 직선의 기울기 구하는 법, 기울기 공식
3. 개념 설명
먼저 기울기의 뜻부터 알아볼까요?
💡 기울기란, 직선이 기울어진 정도를 나타내는 수에요.
그림으로 쉽게 설명해 드릴게요.

세 가지 직선은 기울어진 정도가 모두 다르죠?
기울어진 정도를 나타내는 기울기도 당연히 다릅니다.
이번엔 직선의 기울기 구하는 법을 알아볼게요.
기울어진 정도(=기울기)를 어떻게 구할 수 있을까요?
x값이 변화할 때 y값은 어떻게 변하는지 파악하면 구할 수 있어요.
무슨 말인지, 아래 직선의 기울기를 구해보며 알아볼까요?

이 직선의 기울기를 구하려면, x값이 변화할 때 y값이 얼마만큼 변하는지 알면 된다고 했죠?
x값이 1만큼 증가할 때,

y값은 2만큼 증가했어요.

x값이 변화할 때 y값의 얼마나 변화하는지는 아래와 같이 분수로 표현할 수 있어요.

*분수가 뭔지 모르는 분들은 아래 글 먼저 보고 와주세요. 아래에도 계속 나옵니다.
분수 뜻, 기호, 읽는 방법
경제학을 공부하려면 분수에 대한 이해는 필수인데요. 초등수학을 공부하지 않은 수포자분들은 이 개념을 정확히 모를 수도 있습니다. 그런 분들을 위해, 아래의 순서로 분수에 대해 알려드릴
helpmathquitter.tistory.com
위에서 봤던 직선의 기울기는 아래와 같이 계산할 수 있어요.

x값이 1만큼 증가할 때 y값이 2만큼 증가했으니까요.
그럼, x값이 2만큼 증가할 때는 y값이 몇 증가할까요?
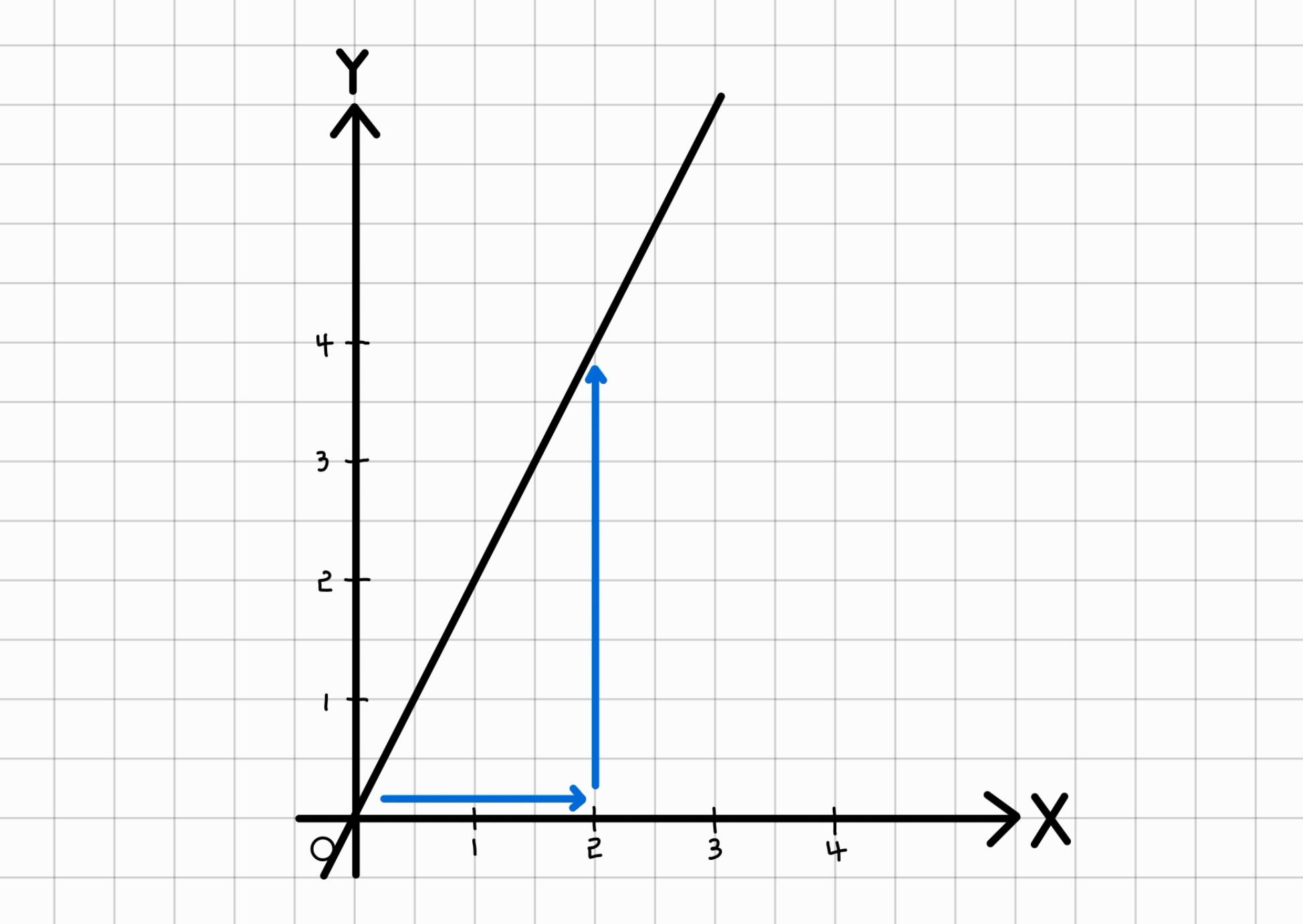
y값은 4만큼 증가했어요.
기울기를 구해볼까요?

기울기는 아까와 같이 2가 나와요.
한 직선의 기울기는 x값을 1만큼 증가시켜도, 2만큼 증가시켜도, 얼마를 변화시키든 같은 값이 나와요.
직선의 기울어진 정도는 일정하기 때문이죠.
즉, 직선을 지나는 두 점을 알면, 기울기를 구할 수 있다는 것인데요.
위의 직선을 다시 한번 가져와 볼게요.
이 직선은 점 (1, 2)와 (2, 4)를 지나요.
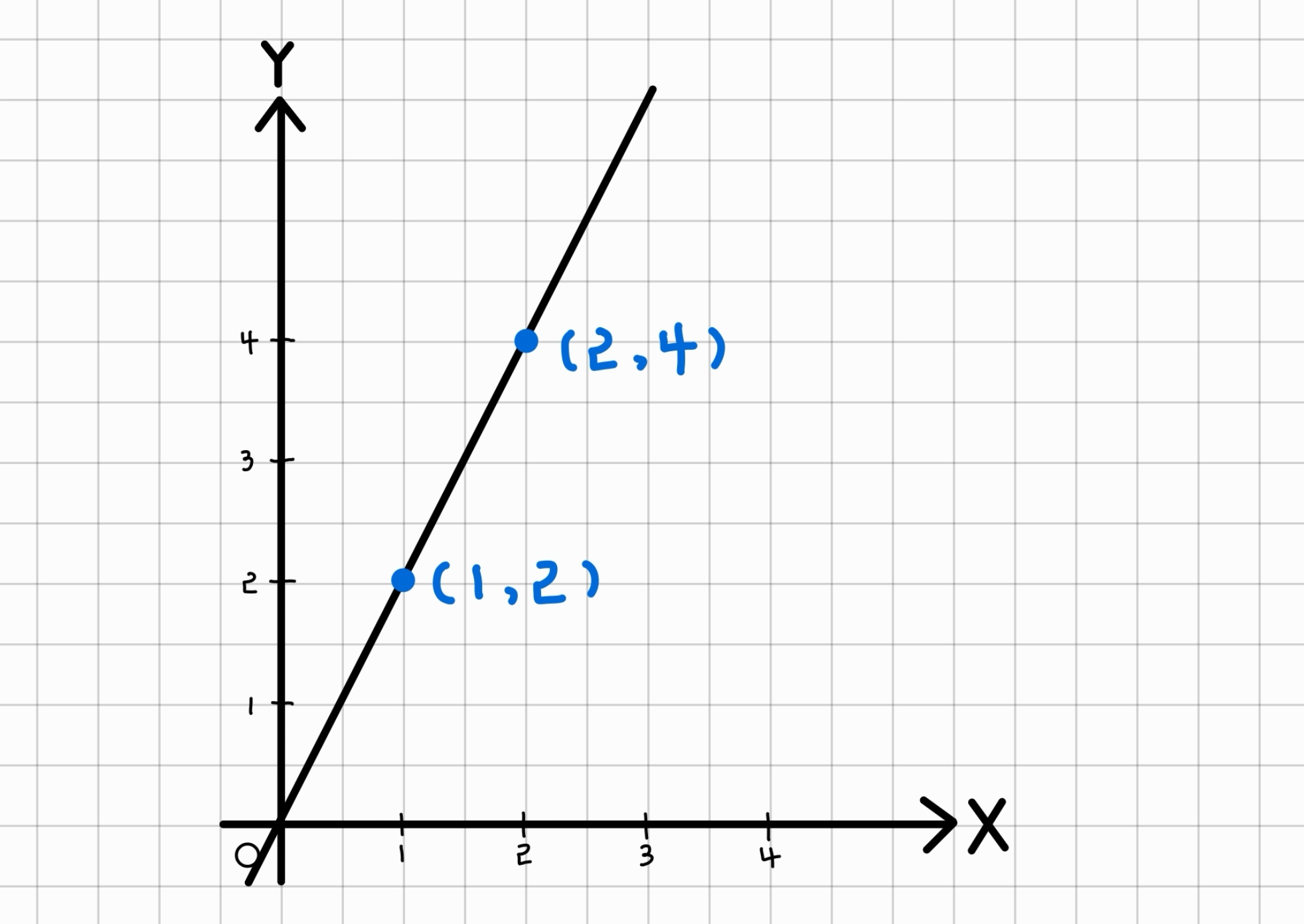
즉, x가 1만큼 증가할 때 y는 2만큼 증가하는 것이죠.

여기서 x의 변화량은 2 - 1 = 1, y의 변화량은 4 - 2 = 2로 알 수 있어요.
즉, 직선이 두 점 (x₁, x₂), (y₁, y₂)를 지날 때 x의 변화량은 x₂ - x₁로, y의 변화량은 y₂ - y₁로 알 수 있다는 것이죠.
이게 직선의 기울기를 구하는 공식이에요.

직선이 두 점 (x₁, x₂), (y₁, y₂)를 지난다는 것을 알면, 위의 공식으로 기울기를 빠르게 구할 수 있습니다.
예시를 통해서 다시 알아볼게요.
두 점 (3, 6), (4, 9)를 지나는 직선의 기울기는 어떻게 구할 수 있을까요?

x₁, x₂, y₁, y₂를 먼저 정해주고,

기울기 공식에 대입하면 됩니다. (대입이 뭔지 모른다면 👉🏻 클릭)
따라서 두 점 (3, 6), (4, 9)를 지나는 직선의 기울기는 3입니다.
이제 문제를 다시 풀어볼까요?
✍️ 문제
①~④ 중 (2, 3), (7, 6)을 지나는 직선의 기울기는?

✔︎ 정답 ③

x₁, x₂, y₁, y₂를 정해주고, 기울기 공식에 대입하면 끝!
공식만 잘 외워두면, 기울기 구하는 것이 어렵지 않을 거예요.
기울기를 구하는 것은 연습이 꼭 필요합니다.
기울기를 이용한 경제 개념이 많이 나오기 때문이죠.
따라서 아래 링크에서 연습문제 PDF파일을 무료로 제공하고 있으니, 연습이 필요하신 분들은 다운받아서 풀어보세요.
기초수학 연습문제 PDF파일 무료 제공
수학 공부가 어려우신가요? 이 블로그에서는 수포자분들도 이해하기 쉽도록, 기초수학 개념을 담은 글을 업로드하고 있어요. 올려드리는 글 중에서는 한 번 스윽 훑어보고 이해하면 되는 개념
helpmathquitter.tistory.com
4. 정리
오늘 배운 내용을 정리해 볼까요?
💡 기울기 - 직선이 기울어진 정도를 나타내는 수
💡 기울기 구하는 방법 - (y값의 변화량) / (x값의 변화량)
💡 기울기 공식 - (y₂ - y₁) / (x₂ - x₁)
오늘은 직선의 기울기에 대해 알아봤어요.
5. 응용문제
오늘 배운 내용을 완벽히 숙지했다면, 아래 문제도 풀 수 있을 거예요.
✍️ 응용문제
①~④ 중 (4, 3), (5, 1)을 지나는 직선의 기울기는?

① 1
② 2
③ -1
④ -2
✔︎ 정답 ④

기울기는 마이너스 값이 나올 수도 있어요.
공식만 잘 기억하시면 됩니다!
추가로, x값의 변화량, y값의 변화량을 델타(𝜟)라는 기호로 간단하게 표현할 수 있어요.
x값의 변화량 = 𝜟x
y값의 변화량 = 𝜟y

즉, 기울기를 이렇게도 표현할 수 있다는 점 기억해 주세요.
이제 직선의 기울기에 대해서 정확히 아시겠나요?
경제학, 기초 수학을 공부하시는 데에 도움이 되었기를 바라며, 오늘 글은 여기서 마칠게요.
궁금한 점은 언제든지 댓글 남겨주세요.
🐣 앞으로도 수포자분들이 경제까지 포기하지 않도록, 경제학에 필요한 수학만 쏙쏙 골라서 알려드리겠습니다.
감사합니다.
'기초수학' 카테고리의 다른 글
| 절대값? 절댓값? 뜻, 기호 (0) | 2025.01.13 |
|---|---|
| 수학 대입하다 뜻 (0) | 2025.01.13 |
| 분수 뜻, 기호, 읽는 방법 (1) | 2025.01.13 |
| 순서쌍 뜻, 그래프 그리는 방법(기초) (0) | 2025.01.10 |
| 좌표, 좌표축, X축, Y축, 원점, 좌표평면 뜻 (0) | 2025.01.09 |



